Kondensator-Anomalie ??

[Ney]

@Kondi

Ich rate dir dringend von dieser Berechnungsart ab!

Zwar ist das Endergebnis korrekt, es sagt aber nicht aus, welche Spannungen sich einstellen und was die Endschaltung in Wirklichkeit ist. Der Kondensator in der Mitte wird am Ende die gleiche Spannung haben, wie die Summe der anderen zwei Spannungen. Das bedeutet, die zwei äußeren sind in Serie geschaltet und parallel zu dem inneren. Somit beträgt die gesamte Kapazität keine 33,3nF, sondern:

(100nF Serie 100nF) || 100nF = 150nF

Durch deinen sog. Kurzschluss tust du die Schaltung nicht belasten, sondern nur für einen Ladungsausgleich sorgen. Deshalb bleiben bestimmte Spannungen auf den 3 Kondensatoren hängen

Nimm das erste Berechnungsbeispiel auf der ersten Seite und ersetze 15V mit eben 10V

[Erfinderlein]

Hallo Kondi,

wenn du den mittleren Kondensator rausnimmst und durch die zwei auf meinetwegen 2cm voneinander entfernten Drahtenden der anderen Kondensatoren ersetzen tust, hast du deinen kleinen Kondensator. Nun erzähl mir mal wie du den Stromfluß nachweisen willst oder gar Spannungsunterschiede messen willst'?

Bevor du Anders "dumm Tüch" an die Backe nähen willst, solltest du dich erst mal gründlichst in deinem ureigenen Metier auskennen. Das würde bedeuten, auch ein spezielles Vorstellungsvermögen zu entwickeln überschüssige Elektronen oder fehlende Elektronen um dich herum zu erschnuppern, ja fast zu sehen.Dieser kleinste Kondensator war diesbezüglich ein gutes Beispiel für fehlgeleitetes Denken mangels zu geringem Vorstellungsvermögen.

Zu wenig ist für gewisse Aufgaben einfach ungenügend. Zugegebenermaßen ist zu viel auch nicht immer gut.

LG²

[anders]

Zu wenig ist für gewisse Aufgaben einfach ungenügend. Zugegebenermaßen ist zu viel auch nicht immer gut.

Ein weises Wort!

[Ney]

Leute,

ich weise noch ein Mal ausdrücklich hin, dass eure Überlegungen total falsch sind!!!

In gewisserweise bin ich auch etwas sauer. Ich habe das Gefühl, meine Zeit und den Aufwand umsonst zu investieren. Es wird eh nicht beachtet. Stattdessen greift ihr auf irgendwelche "Zaubereien", die mit den Grundlagen der Physik und Mathematik absolut nichts zu tun haben. Gebt euch keine Medaillen, dafür ist es vieeeel zu früh. Ich lade euch hiermit erneut ein, scharf nachzudenken und los gehts:

@anders:

Du kommst zwar auf das richtige Ergebnis, aber mit einer falschen Überlegung. Das klingt zunächst verwirrend, aber die Erklärung hängt mit einem arithmetischen Zufall zusammen.
Gehen wir doch zu meinem Beispiel auf der ersten Seite zurück. Ich hatte dort hergeleitet, dass jeder der 3 Kondensatoren ein DeltaU = 5V in der Spannung beim Ladungsausgleich verliert. In deinem Beispiel war die Klemmenspannung 10V, also wäre DeltaU auch ein drittel dieser Spannung
=> DeltaU = 10V/3 = 3,33V
Die Sache mit dem Drittel ist wichtig zu merken. Ein Drittel kommt hier deshalb zustande, weil alle 3 übrigen Kondensatoren gleich sind!!!
Man könnte sagen, dass jeder der 3 übrigen Kondensatoren eine Energie abgibt, die sich wie folgt darstellen lässt:

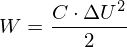
Diese 3 Energien sind gleich, da alle Kondensatoren gleich sind
Durch ersetzen von DeltaU als Klemmenspannung (Remember, ein Drittel):

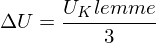
bekommen wir für jeden Kondensator folgende Energieabgabe:
Wk = mit k = 1...3

Das bekommen wir 3 mal in Summe und genau jetzt kommt der Clou:


Eine 3 kürzt sich ab und eine einzige 3 bleibt übrig:


Man sieht, dass die Schreibweisen links und rechts in der letzten Gleichung mathematisch identisch sind, aber nicht das gleiche bedeuten. Im linken Teil ist ein drittel der Klemmenspannung gemeint. Das ist auch korrekt, da alle 3 übrigen Kondensatoren den gleichen Wert haben. Im rechten Teil dagegen sieht es so aus, als ob die Kapazität durch 3 geteilt wird, was bei einer Serienschaltung mit 3 gleichen Kondensatoren auch wirklich der Fall wäre. Die Multiplikation mit der Klemmenspannung liefert den Rest und die Falle schanppt zu.

Es sieht so aus, als ob die Serienschaltung in dieser Betrachtung die koreekte Lösung sei. Das ist falsch, da eine Serienschaltung die gleiche Ladung Q auf allen Kondensatoren vorsieht und ich habe auch erklärt warum. Es fließt der gleiche Strom durch eine Serienschaltung. In diesem Fall aber, wird ein Kondensator aus der Mitte entfernt, was bei einer Parallelschaltung bedeutet, dass ein Teil der gesamten Ladung weggenommen wird. Die 3 Kondensatoren waren ohnehin nicht als direkte Serienschaltung verschaltet und würden beim verbinden der äußeren Klemmen auch nicht vollständig die Ladung abgeben. Aus diesem Grund greift hier deine Betrachtung nicht.
In Wirklichkeit, nachedem die äußeren Klemmen zusammengeschlossen werden, sind die äußeren Kondensatoren seriell geschaltet und der mittige parallel dazu. In meinem Beispiel ist so die Endspannung 2V

Es ist erneut die Zeit zu sagen, denk scharf nach!
Mach bitte eine Berechnung mit 4 völlig unterschiedlichen Kondensatoren. Dann wirst du erst sehen, dass dieser rein zufällige arithmetische Fall nicht mehr gegeben ist

[anders]

Man könnte sagen, dass jeder der 3 übrigen Kondensatoren eine Energie abgibt, die sich wie folgt darstellen lässt:

Diese 3 Energien sind gleich, da alle Kondensatoren gleich sind

Und das ist falsch, deltaU gehört da nicht hin!
Diese Formel gilt nur, wenn der Kondensator seine Spannung zwischen 0 und U verändert.
Es ist etwas völlig Anderes, ob man einen Kondensator von 5V auf 0V entlädt, oder von 105V auf 100V.

Man braucht wirklich nicht das Innenleben der Blackbox zu kennen. Für die Berechnung der entnehmbaren Energie reicht es völlig die Kapaziät und die Klemmenspannung zu wissen.

Es ist erneut die Zeit zu sagen, denk scharf nach!

Ja, tu das!

[Ney]

Und das ist falsch, deltaU gehört da nicht hin!
Diese Formel gilt nur, wenn der Kondensator seine Spannung zwischen 0 und U verändert.
Es ist etwas völlig Anderes, ob man einen Kondensator von 5V auf 0V entlädt, oder von 105V auf 100V.

Die 3 Kondensatoren sind nicht auf Klemmenspannung aufgeladen und der Endpunkt ist das Gleichgewicht.

Ähnliches Gedankenspiel: Ein 10uF Kondensator wird auf 10V aufgeladen. Nachher wird er von der Quelle getrennt und mit einem lehren 10uF Kondensator verbunden. Welche Anfangsenergie hat der erste Kondensator, welche Endenergie hat die Parallelschaltung und welche Energie hat der erste Kondensator abgegeben?

[Erfinderlein]

SO, so,

inzwischen ist jeder etwas sauer. Selbst schuld sag ich nur. Wenn der Fragesteller sich mit so einer Äußerung outet, sollte kein Grund mehr dafür da sein weiter über daseigentlich gar nicht existierende Problem nachzudenken.
"Hallo,
danke für eure Überlegungen.
Eine mathematische Berechnung ist für mich uninteressant, da ich eine Anomalie vermute, die mathematisch nicht berechnet werden kann. Ich halte praktische Versuche für aussagekräftiger.
Leider habe ich kein Leistungsmessgerät, mit dem ich prüfen kann welche Leistung die besagte Schaltung erst ohne und dann mit Entnahme eines mittigen Kondensators liefert.

Mir ist klar, dass die Vorgänge in den mittigen Kondensatoren auf Influenz beruhen, deshalb ja auch die Umladung bei nur einem mittigen Kondensator.

Gedankenspiel: Wenn ich die Gesamtschaltung lade, transportiere ich 1000 Elektronen auf eine Kondensatorplatte. Beim Entladen werden wieder 1000 Elektronen zurückgeliefert (im Idealfall), egal ob ein oder zwei mittige Kondensatoren vorhanden sind – Grund ist Influenz.
Folglich bleibt der Elektronenstrom gleich, nur die Spannungen ändern sich, somit auch der zeitliche Ablauf, aber auch die Leistung ???

Da zerfleischt ihr euch und alles um Kaisers Bart.

LG²

[der mit den kurzen Armen]

Ich kann dazu nur sagen, das man nicht dümmer wird! Und wenn man ein Problem anders angeht ergibt sich auch eine neue Sichtweise auf das Problem. Kleines Beispiel von Anders 2 gleiche Kondensatoren in Reihe geschaltet und geladen. Danach wird die äußere Spannung abgeklemmt und ein Kondensator umgepolt wieder in Reihe geschaltet. Beide Kondensatoren tragen ihre Ladung noch, aber an den Außenklemmen ist keine Spannung vorhanden. Demzufolge kann auch kein äußerer und auch kein innerer Ladungsausgleich stattfinden. Die zugeführte Energie ist aber immer noch im Feld zwischen den Platten gespeichert. Ergo gilt der Energieerhaltungssatz weiter. Selbst durch ein weiteres Laden dieser neuen Reihenschaltung bleibt die Energie erhalten und es kann nur die zusätzliche Energie entnommen werden. Das böse Erwachen kommt aber in dem Moment wo die Umpolung wieder rückgängig gemacht wird, dann ist plötzlich aus dem Nichts wieder Spannung auf der Reihenschaltung! Meinen Denkfehler habe ich für mich gefunden danke Ney Hat zwar etwas gedauert bis der "Groschen" gefallen ist. (Reihenschaltung Q= überall gleich , Parallelschaltung Qges =Q1+Q2+..... )

[Kondi]

@Erfinderlein
Halte dich doch einfach aus dem Thema raus und mach dich nicht weiter selbst lächerlich.
Übrigens: Zwei nebenander liegende Leiter in einem Gleichstromkreis bilden keinen Kondensator. LG³ ABER gegenüberliegende schon ! LG³

-Grundlagen der Elektronik

Kondi

Wo ich mich raus oder rein halte geht dich NIX an. Oder soll ich dir Beine machen?

[anders]

Zwei nebenander liegende Leiter in einem Gleichstromkreis bilden keinen Kondensator.

Nee ist schon klar, das ist allenfalls eine Stolperfalle.

@Erfinderlein
Halte dich doch einfach aus dem Thema raus und mach dich nicht weiter selbst lächerlich.

Genial!
Darauf muss man erst einmal kommen, wenn man selbst weder eine Kapazität noch ein Leiter ist, sondern allenfalls Baumschüler.

[der mit den kurzen Armen]

@Erfinderlein
Halte dich doch einfach aus dem Thema raus und mach dich nicht weiter selbst lächerlich.
Übrigens: Zwei nebenander liegende Leiter in einem Gleichstromkreis bilden keinen Kondensator.
-Grundlagen der Elektronik

Kondi

Klar doch und 2 parallele Platten sind auch kein Kondensator ! Junge lern die Grundlagen und zügle deinen Ton !
Was denkst du warum eine Hochspannungsgleichstromleitung selbst nach dem allpoligem Abschalten noch eine gewaltige Spannung trägt! Wenn du so genau über Kondensatoren Bescheid weist dann erkläre mal warum bei Hochspannungsleitungen die Anordnung der Leiter auf den Masten in regelmässigen Abständen vertauscht werden!
Nur zum Nachdenken: Erfinderlein, Anders und auch Ney stehen mindestens 10 Stufen im Wissen über Dir!

[BernhardS]

Kann ich für 10 Minuten den Status Moderator wieder bekommen? Dann löche ich den ganzen Thread

[Erfinderlein]

Hallo BernhardS,

wir wollen solche Dinge nicht gleich löschen, sondern als schlechte Beispiele stehen lassen. Gegebenenfalls werde ich solche threads mit Kommentar versehen und schliessen. Vielleicht machen wir auch in einiger Zeit so ein Unterforum auf, namens "Nit möglich" um solche Stilblüten zumindest ausschnittsweise zu sammeln.

LG Lothar

P.S.: Deine Möglichkeiten wären das Verschieben in den Papierkorb und das Sperren des Mitgliedes. Würde ich aber derzeit von abraten. Die Moderatoraktivitäten wurden ja nach dem Besitzwechsel stark eingeschränkt.

[Kondi]

@Eppelein
Danke für deinen Hinweis

@Ney
Vergesse meine vorherigen Berechnungen.
Bei praktischen Tests mit der Schaltung stellte ich ja fest, dass nach der Entladung der Gesamtschaltung der mittige Kondensator wieder geladen war, nur gegenpolig. Schon da hätte mir klar sein müssen, dass nur die Energie von C1 und C4 abgegeben wurde.
Ich habe mich nochmal mit der elementaren Funktionsweise eines Kondensators beschäftigt, vor allem mit den Vorgängen bei einer Reihenschaltung. Influenz, also die Ladungsverschiebung, ein elementarer Vorgang bei der Reihenschaltung von Kondensatoren, ist die Ursache der Umladung.
Dann berechnete ich die Energieabgabe der Schaltung über die Ladung Q.

Zum besseren Verständnis merkte ich mir:
M1: (Q=I*t) Strom ist definiert als "Elektronen pro Zeiteinheit“. Somit gilt auch: Q=n (n=Anzahl der Elektronen).
M2: Innerhalb der Reihenschaltung bewirkt die Ladung Q eine Spannung, nicht umgekehrt (mit C).

Schaltungsaufbau ist bekannt
Spannung: 10 V
Kondensatoren: C1;C2;C3;C4 je 1 F = Gesamtkapazität : 0,4 F
------------------------------------------------------------
1.Nach dem Aufladen
Gesamtenergie (W=1/2*C*U²): 20 Ws
Ladung Q (Q=C*U): 4 C
Spannung (U=Q/C) an C1: 4 V ; an C2 und C3: 2 V ; an C4: 4 V
Energie (W=1/2*C*U²): in C1 und C4: jeweils 8 Ws ; in C2 und C3 jeweils 2 Ws = 4 Ws
------------------------------------------------------------
2.Entnahme des mittigen Kondensators C3
Entnommene Energie (W=1/2*C*U²): 2 Ws
Nun ist die Ladung Q C1: 4 C ; C2: 2 C ; C4: 4 C
Spannungen wie bei 1.
Gesamtenergie: 20 Ws – 2 Ws von C3 = 18 Ws
------------------------------------------------------------
3.Teilentladung bis C2 entladen ist
Nun ist die Ladung Q C1: 2 C ; C2: 0 C ; C4: 2 C
Zur ‚kompletten‘ Entladung der Schaltung muss C2 aber noch 2 C Ladung (Q=n) verschieben.
Hier beginnt die gegenpolige Aufladung (siehe M2).
------------------------------------------------------------
4.Schaltung ‚komplett‘ entladen
Nun ist die Ladung Q C1: 0 C ; C2: (-)2 C ; C4: 0 C
Spannung (U=Q/C) an C1: 0 V ; an C2: (-)2 V ; an C4: 0 V
Energie (W=1/2*C*U²): in C1 und C4: jeweils 0 Ws ; in C2: 2 Ws
------------------------------------------------------------
Die Energie von C2 wurde nicht abgegeben, nur die Energie von C1 und C4, also 16 Ws.
16 Ws sind 80 % der zugeführten Energie.

Durch diese simple Berechnungsart über die Ladung umgehe ich mein bisheriges Problem mit der Gegenspannung bei C2.
Zur weiteren Vereinfachung können die ganzen Zwischenberechnungen weggelassen werden.
In Tabellenform gebracht werden die Berechnungen noch einfacher.

Vielleicht ist dir dies hilfreich.

LG
Kondi

[Ney]

Dann löche ich den ganzen Thread

Und dann war die Mühe völlig umsonst, oder wie?

@Kondi

Du hast schon wieder einen Fehler in der Überlegung und das geht ab Punkt 3. C1 und C4 können sich nicht vollständig entladen. Ansonsten wird die Maschengleichung nicht erfüllt. Die Summe aller Spannungen muss Null sein. Überleg doch mal, vom Knoten zum Knoten gab es Q = 4µCoulomb. Durch Herausnahme von C3 bleibt C2 mit nur 2µCoulomb. Auf genau diesen Wert wird sich die gesamte Schaltung einstellen. Da C1 und C4 die gleiche Ladung besitzen, werden sie die neue Ladung als Serienschaltung vorweisen.
Die Schaltung sieht dann so aus: (C1 in Serie zu C4)||C2
Wir haben folgende Gleichungen:
1) Q1 = 0,5µF x U --> Ladung der Serienschaltung C1 und C4
2) Q2 = 1µF x U --> Ladung des Kondensators C2
3) Q1+Q2 = 2µC

1) und 2) in 3) => 0,5µF x U + 1µF x U = 2µC => U = 1,3 (Periodisch)
Aus 2) => Q2 = 1µF x 1,3V = 1,3µCoulomb
Aus 1) => Q1 = 0,5µF x 1,3V = 0,6µC

Also, die sich einstellende Spannung ist -1,3V auf C2 und +1,3V auf C1 und C3
Die Summe ist Null
Restenergie: 1,3V x 2µCoulomb/2 = 1,3 µJoule